A stack, also known as a stack, is a special ordered list whose insertion and deletion operations are performed on the top of the stack and operate in accordance with advanced, last-in, first-out rules.
As shown below
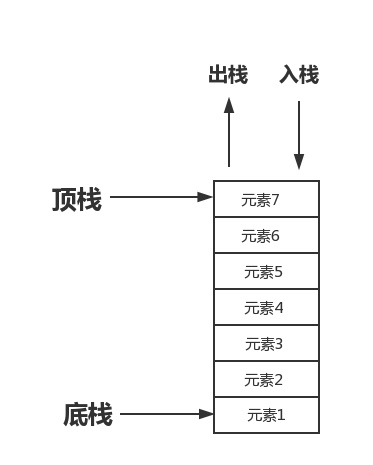
For example, the bullet of the gun, the first bullet placed in the magazine is the last one when it is launched, and the last bullet placed in the magazine is the first to be launched when it is shot.
Stack interface
If you create a stack, then you should have the following interface to operate on the stack.
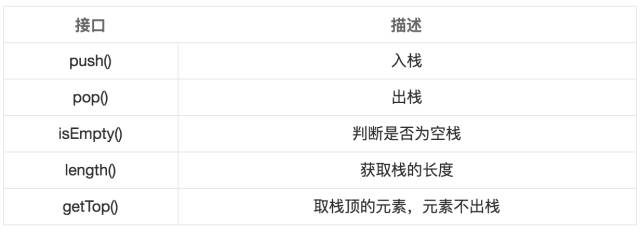
Knowing that the stack requires the above interface, then in Python, the list is similar to a stack, providing the interface as follows:
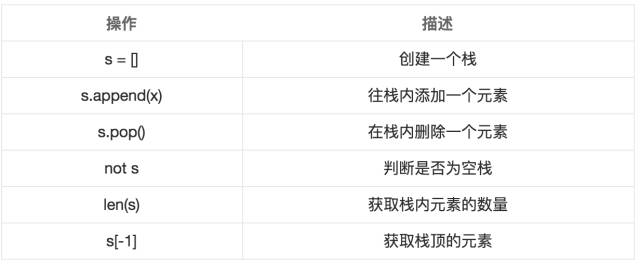
An example of a stack interface in Python:
#Create a stack
In[1]: s = []
# Add an element to the stack
In[2]: s.append(1)
In[3]: s
Out[3]: [1]
# Delete an element in the stack
In[4]: s.pop()
Out[4]: 1
In[5]: s
Out[5]: []
# Determine if the stack is empty
In[6]: nots
Out[6]: True
In[7]: s.append(1)
In[8]: nots
Out[8]: False
# Get the number of elements in the stack
In[9]: len(s)
Out[9]: 1
In[10]: s.append(2)
In[11]: s.append(3)
#å–å–顶顶的元ç´
In[12]: s[-1]
Out[12]: 3
a large wave of instances
After understanding the basic concepts of the stack, let's look at a few more examples to understand the stack.
Bracket matching
topic
If the expression allows three brackets (), [], {}, the order of nesting is arbitrary, for example:
Correct format
{()[()]},[{({})}]
Wrong format
[(]), [()), (()}
Write a function that determines an expression string and whether the parentheses match correctly
Thought
Create an empty stack to store the left parentheses that have not been found;
Convenience string, when the left parenthesis is encountered, the stack is pushed, and when the right parenthesis is encountered, a left parenthesis is popped to match;
In the second step, if the right parenthesis is encountered in the case of an empty stack, the left parenthesis is missing and does not match;
At the end of the second step traversal, the stack is not empty, indicating that the right parenthesis is missing and does not match;
Solution code
It is recommended to break points in pycharm for better understanding.
#!/use/bin/env python
# _*_ coding:utf-8 _*_
LEFT = {'(','[','{'} # left parenthesis
RIGHT = {')',']','}'} # å³
Defmatch(expr):
"""
:param expr: passed over the string
:return: Returns whether it is correct
"""
Stack = [] # create a stack
Forbrackets inexpr: # iterate over all strings
Ifbrackets inLEFT: # if the current character is in the left parenthesis
Stack.append(brackets) # put the current left parenthesis on the stack
Elifbrackets inRIGHT: #if it is the right parenthesis
Ifnotstack ornot1 <= ord(brackets) - ord(stack[-1]) <= 2:
# If the current stack is empty, ()]
# If the value of the closing parenthesis minus the left parenthesis is not less than or equal to 2 is greater than or equal to 1
returnFalse # return False
Stack.pop() # Remove left parenthesis
Returnnotstack # Returns True if there is no value in the stack, otherwise returns False
Result = match('[(){()}]')
Print(result)
Labyrinth problem
topic
Use a two-dimensional array to represent a simple labyrinth, with 0 for the path, with 1 for blocking, and at each point the mouse can move to the adjacent southeast and northwest four points, design an algorithm that simulates the mouse walking the maze and finds A path from the entrance to the exit.
as the picture shows
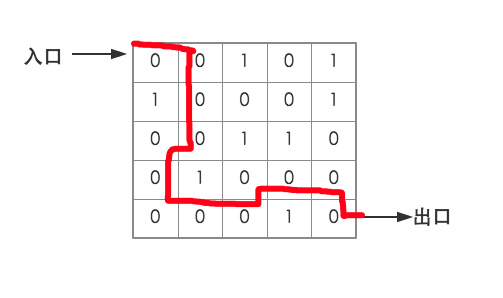
The correct line to go out is shown by the red line in the figure.
Thought
Use a stack to record the path of the mouse from the entrance to the exit
After going to a certain point, push the left side of the point and set the value to 1, indicating that it has passed;
Select one of the four points that can be reached from the adjacent four points and go to that point;
If you don't leave the 4 points when you reach a certain point, it means you have entered the dead end. At this time, you will withdraw from the stack and return to try another point.
Repeat the second, third, and fourth steps until the exit is found;
Solution code
#!/use/bin/env python
# _*_ coding:utf-8 _*_
definitMaze():
"""
:return: Initialize the maze
"""
Maze = [[0] * 7for_inrange(5 + 2)] # Create a 7*7 2D array with list resolution, in order to ensure that the maze is surrounded by walls
Walls = [ # Record the location of the wall
(1,3),
(2,1), (2,5),
(3,3), (3,4),
(4,2), # (4, 3), # If the (4, 3) point is also set to the wall, then the entire labyrinth can't go out, so it will return an empty list.
(5,4)
]
Foriinrange(7): # Set the perimeter of the maze into a wall
Maze[i][0] = maze[i][-1] = 1
Maze[0][i] = maze[-1][i] = 1
Fori,jinwalls: # Set all wall points to 1
Maze[i][j] = 1
Returnmaze
"""
[1, 1, 1, 1, 1, 1, 1]
[1, 0, 0, 1, 0, 0, 1]
[1, 1, 0, 0, 0, 1, 1]
[1, 0, 0, 1, 1, 0, 1]
[1, 0, 1, 0, 0, 0, 1]
[1, 0, 0, 0, 1, 0, 1]
[1, 1, 1, 1, 1, 1, 1]
"""
Defpath(maze,start,end):
"""
:param maze: maze
:param start: starting point
:param end: end point
:return: every point of walking
"""
i,j = start # The coordinates of the decomposition starting point
Ei, ej = end # The left side of the decomposition end point
Stack = [(i,j)] # Create a stack and let the mouse stand at the starting point
Maze[i][j] = 1 # The path passed is set to 1
Whilestack: # Continue to go when the stack is not empty, otherwise exit
i,j = stack[-1] # Get the position of the current mouse station
If(i,j) == (ei,ej): break # If the mouse finds the exit
Fordi,dj in[(0, -1),(0,1),(-1,0),(1,0)]: #å·¦å³å·¦å³
Ifmaze[i + di][j + dj] == 0: # If the current point is OK
Maze[i + di][j + dj] = 1 # Set the current point to 1
Stack.append((i + di,j + dj)) # Add the current location to the stack
Break
Else: # if all points are not allowed
Stack.pop() # Return to the previous step
Returnstack # Returns an empty stack if the maze cannot go
Maze = initMaze() # Initialize the maze
Result = path(maze=Maze,start=(1,1),end=(5,5)) # The mouse starts to walk the maze
Print(result)
# [(1, 1), (1, 2), (2, 2), (3, 2), (3, 1), (4, 1), (5, 1), (5, 2), (5, 3), (4, 3), (4, 4), (4, 5), (5, 5)]
Postfix expression evaluation
topic
When evaluating an expression, the compiler usually uses a suffix expression that does not require parentheses:

Write a program to implement the suffix expression evaluation function.
Thought
Establish a stack to store the operands to be calculated;
Traversing the string, it is pushed onto the stack when it encounters the operand, and the stack operand (n times) is encountered when the operation symbol is encountered, and the corresponding calculation is performed. The calculation result is that the new operand is pushed back into the stack and waits for calculation.
According to the above process, traversing the complete expression, only the final result is left in the stack;
Solution code
#!/use/bin/env python
# _*_ coding:utf-8 _*_
Operators = { # operator operation table
'+': lambdaop1, op2: op1 + op2,
'-': lambdaop1, op2: op1 - op2,
'*': lambdaop1, op2: op1 * op2,
'/': lambdaop1, op2: op1 / op2,
}
defevalPostfix(e):
"""
:param e: postfix expression
:return: Normally the first element in the stack is the value after the calculation
"""
Tokens = e.split() # Divide the passed suffix expression into a list
Stack = []
Fortokenintokens: # Iterate the elements in the list
Iftoken.isdigit(): # if the current element is a number
Stack.append(int(token)) # is appended to the stack
Eliftokeninoperators.keys(): # If the current element is an operator
f = operators[token] # Get the corresponding lambda expression in the operator operation table
Op2 = stack.pop() # According to the principle of advanced output, let the second element pop up first.
Op1 = stack.pop() # put the first element on the stack
Stack.append(f(op1,op2)) # put the result of the calculation into the stack
Returnstack.pop() # returns the first element in the stack
Result = evalPostfix('2 3 4 * +')
Print(result)
# 14
Backpack problem
topic
There is a backpack that can hold 10kg items, and now there are 6 items:
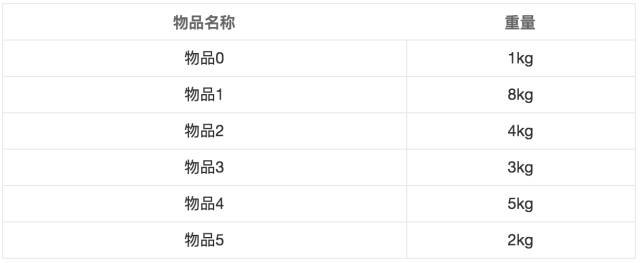
Write to find out all the solutions that can pack the back, such as item 1 + item 5.
Solution code
#!/use/bin/env python
# _*_ coding:utf-8 _*_
Defknapsack(t,w):
"""
:param t: total backpack capacity
:param w: item weight list
:return:
"""
n = len(w) # Optional number of items
Stack = [] # create a stack
k = 0 # currently selected item cursor
Whilestack ork < n: # stack is not empty or k Whilet > 0andk < n: # There is still space left and items can be loaded Ift >= w[k]: # The remaining space is greater than or equal to the current item weight Stack.append(k) #装备用å“装备 t -= w[k] # Backpack space reduction k += 1 # Continue looking backwards Ift == 0: # Find out Print(stack) #回退过程 k = stack.pop() # Take the last item out t += w[k] # total backpack capacity plus w[k] k += 1 # Load the next item Knapsack(10,[1,8,4,3,5,2]) """ [0, 2, 3, 5] [0, 2, 4] [1, 5] [3, 4, 5] """ Tpd Compliant Vapes,Original Onlyrelx Vape,Disposable E-Cigarette Onlyrelx,Vapeorizer Pen Shenzhen Onlyrelx Technology Co.,Ltd , https://www.onlyrelxtech.com