A brief introduction to MEMS gyroscopes (performance parameters and usage)

The MEMS sensor market wave can range from the earliest automotive electronics to consumer electronics in recent years, and the upcoming Internet of Things era. Nowadays, a single sensor can no longer meet the needs of people's functions and intelligence. The fusion of various sensor data, including MEMS inertial sensors, MEMS environmental sensors, MEMS optical sensors and even biosensors, will become the trend of sensor applications in the new era.

If you want to do something good, you must first sharpen it. Here, let's start with a MEMS gyroscope. Briefly introduce the MEMS gyroscope, main performance parameters and use.

Conventional mechanical gyroscopes mainly use the principle of conservation of angular momentum, that is, for a rotating object, its axis of rotation does not change with the rotation of the bracket carrying it. MEMS gyroscopes mainly use the principle of Coriolis force (the tangential force of rotating objects when they have radial motion). The disclosed micromechanical gyroscopes use the concept of sensing angular velocity of vibrating objects, using vibration to induce and detect. Coriolis force.

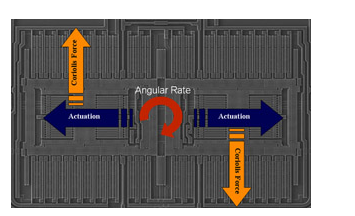
At the heart of the MEMS gyroscope is a micromachined mechanical unit that is designed to resonate in accordance with a tuning fork mechanism to convert the angular rate into a displacement of a particular sensing structure using the Coriolis force principle. Taking a single-axis offset (yaw, YAW) gyroscope as an example, the simplest working principle is explored through Tuli.

Two identical masses are oscillated horizontally in opposite directions, as indicated by the horizontal arrow. When an angular rate is applied externally, a Coriolis force appears, the direction of the force being perpendicular to the direction of mass motion, as indicated by the vertical arrow. The resulting Coriolis force shifts the sense mass, which is proportional to the magnitude of the angular rate applied. Since the moving electrode (rotor) of the sensing portion of the sensor is located on the side of the fixed electrode (stator), the above displacement will cause a change in capacitance between the stator and the rotor, and therefore, the angular rate applied at the input portion of the gyroscope is Converted into an electronic circuit that can be detected by a dedicated circuit -- capacitance.

The following figure shows the system architecture of a MEMS gyroscope. The signal conditioning circuit of the gyroscope can be divided into two parts: the motor drive and the accelerometer sensing circuit. Wherein, the motor driving part is driven by an electrostatic priming method to vibrate the driving circuit back and forth to provide excitation for the mechanical component; and the sensing part measures the displacement of the Coriolis force in the sensing quality by measuring the capacitance change.

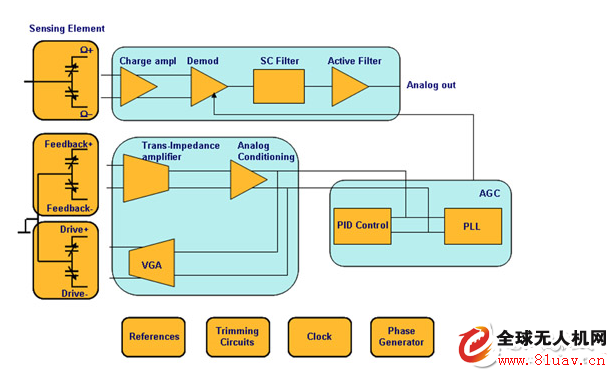
Of course, MEMS gyroscopes also have other functional modules, such as self-test function circuits, low power consumption, and motion wake-up circuits.

The main performance parameters of the MEMS gyroscope are mainly described below.

Range (dynamic range) DYNANMIC RANGE

Sensitivity SENSORRTIVITY RESOLUTION

Zero angular speed output (zero output) ZERO OUTPUT

Inter-axis intermodulation sensitivity INTER AXIS sensitivity

Scale factor

Nonlinearity

Linear acceleration sensitivity

Vibration sensitivity

Zero offset stability

Noise density

Angle free walk system

bandwidth

Bias voltage sensitivity

Self-test function

Power consumption

Impact survivability

range of working temperature

Package error

The range of the gyroscope is usually expressed as the maximum value of the input angular rate in the positive and negative directions, for example: +/- 300 degree/sec. The larger the value, the stronger the ability of the gyroscope to measure the angular rate. In this range of input angular rates, the gyroscope scale factor nonlinearity can meet the specified requirements. Generally, the gyroscope's range is configurable.

Sensitivity (resolution) represents the increment of the minimum input angular rate that can be sensed at a specified input angular rate, such as: 0.05 degree/sec/LSB. In general, the larger the measurement range of the MEMS gyroscope, the lower the sensitivity.

The scale factor (scale factor) is the ratio of the gyroscope output to the input angular rate. This ratio is represented by a specific straight line slope that is obtained by least squares fitting based on input and output data measured over the entire range of input angular rates.

The degree of nonlinearity is the ratio of the maximum deviation of the gyro output relative to the maximum output in the range of the input angular rate, which is the ratio of the deviation of the actual input and output data of the gyroscope. The credibility of the data.

The linear acceleration sensitivity reflects the gyroscope's sensitivity to acceleration in degrees/sec/g.

Vibration sensitivity refers to the sensitivity of the gyroscope to vibration, and the unit is degree/sec/g2. The less sensitive the gyroscope is to linear acceleration and vibration, the better the performance of the gyroscope and the more efficient the algorithm is.

The zero bias refers to the output of the gyroscope in the zero input state, which is expressed by the equivalent of the longer-term output equivalent to the input angular rate, that is, the degree of dispersion of the observed value around the zero offset, for example, 0.005 degree/sec means that The second will float 0.005 degree. The long-term steady-state output in the zero-input state is a stationary stochastic process, that is, the steady-state output will revolve around the mean (zero-bias) fluctuations and fluctuations, which are conventionally expressed by the mean square error, which is defined as a zero-bias stability. The initial zero offset error can be understood as a static error, it does not fluctuate over time, and software calibration can be used.

When the gyroscope is in the zero input state, the output signal that is off is a superposition of white noise and a slowly varying random function. The creep random function can be used to determine the zero offset and zero offset stability indicators. White noise is defined as the standard deviation of the equivalent rotational angular velocity in the square root of the unit detection bandwidth (degree/sec/√Hz or degree/hr/√Hz). This white noise can also be expressed by an arbitrary walking coefficient in degrees of degree/√Hz. The random walking coefficient refers to the gyroscope output error coefficient accumulated by time generated by white noise. When the external conditions are basically unchanged, it can be considered that the main statistical characteristics of the various noises analyzed above do not change over time.

The bias voltage sensitivity refers to the sensitivity of the output of the gyroscope to the power supply change, for example: 0.03degree/sec/V, that is, the output angular rate changes every time the power supply changes by 1V.

Bandwidth refers to the frequency range in which the gyroscope can accurately measure the angular rate of the input. The larger the range, the stronger the dynamic response of the gyroscope.

The self-test feature automatically tests the mechanical and CMOS circuit portions of the device prior to use to provide system robustness.

Power consumption includes power consumption when the gyroscope is operating at different resolutions or different data output rates, and sleep power consumption. This indicator is especially important in low-power applications such as wearables and IoT applications.

Impact survivability refers to the ability of the gyroscope to withstand different degrees of acceleration shock. For example, the gyroscope after 2000g acceleration shock ensures that the system works normally. This indicator is especially important considering that the application environment of the gyroscope may receive a large impact. Generally, the gyroscope will be hung up beyond its acceleration range, and must be restarted before it can work normally.

The mechanical architecture of a MEMS gyroscope determines that temperature affects the output of the data, and exceeding the operating temperature range can cause large deviations in the data output.

The package error is the angle between the diagonal of the die and the diagonal of the package.