Summary:
Anti-collision algorithm is one of the key technologies of radio frequency identification (RFID). Based on the Q-value anti-collision algorithm of the EPC Gen2 standard, the InnerQ algorithm was proposed. By using the method of reprocessing collision time slots, the problem of repetitive transition of the Q value of the original algorithm was solved, and the system throughput rate was improved, breaking the ALOHA algorithm. The bottleneck with a maximum throughput of 36.8% improved the performance of RFID systems.
0 Preface
Radio frequency identification (RFID) is a wireless communication technology that can identify specific targets and read and write related data through radio signals [1]. The radio frequency communication part of the RFID system includes a reader and a tag. When multiple RFID tags are returned to the reader within the reader's electromagnetic energy coverage area, the reader cannot correctly identify any tag information. This phenomenon is called It's a tag collision.
At present, the anti-collision algorithm used in the international general standard EPC Gen2 can be used to solve the label collision problem. EPC Gen2 algorithm is based on ALOHA class algorithm. It has good adaptability, simple implementation and low recognition delay, but its disadvantage is low throughput. Some of the previous articles have optimized the EPC Gen2 anti-collision algorithm, and the throughput rate has been improved, but it has been difficult to achieve, and many articles have failed to break through. In the case of a large number of tags, the throughput rate is only 36.8%. Bottleneck [2-4].
The optimization scheme proposed in this paper analyzes the characteristics and performance of EPC Gen2 algorithm and Dynamic Frame Slotted ALOHA (DFSA) [5], and proposes the InnerQ algorithm, which still keeps the ALOHA algorithm easy. The advantages realized are that the number of tag collision time slots is reduced, and the system throughput rate is improved at the same time, breaking the bottleneck of 36.8%.
1 Research status
1.1 Introduction to DFSA Algorithm
The DFSA algorithm is an algorithm that can dynamically adjust the frame length so that the frame length is close to the number of tags to be identified and the system throughput rate is kept as high as possible. When the frame length is equal to the number of tags to be identified, the system throughput rate reaches a maximum, and when the number of tags is much greater than 1, the peak value of the throughput rate remains at 36.8%. The proof process can be found in [6].
1.2 Introduction to EPC Gen2 Algorithm
The anti-collision algorithm in the EPC Gen2 standard is also a special DFSA algorithm. The algorithm is defined by the reader for a certain length of time (including several time slots). When the tag receives the corresponding command, it randomly selects a time slot for access. The reader writer adjusts the value of the time slot counter in the tag through a combination of instructions such as Query, QueryRep, and QueryAdjust, and responds when the tag counter value is zero. Contains multiple frames in an inventory cycle. The EPC Gen2 anti-collision algorithm can dynamically adjust the frame length at any point in the inventory process, allowing the unidentified tag to enter the next frame's response cycle [7].
1.2.1 Steps to Implement EPC Gen2 Anti-collision Algorithm
The algorithm flow is shown in Figure 1. The specific implementation steps are as follows:
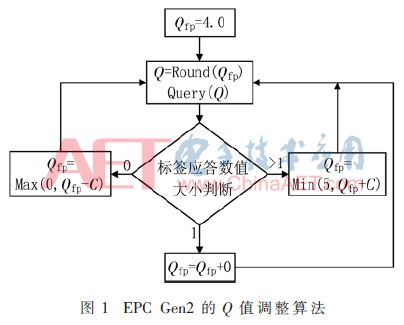
(1) Q initial value is set to 4. The reader issues a Query (Q) instruction to start an inventory cycle.
(2) The tag will generate a random number in the range [0, 2Q-1] to be loaded into the tag slot counter. At the same time, 2Q is loaded into the reader slot counter at the reader end to record the current frame length remaining number of slots.
(3) The tag slot counter responds with a value of 0. If the current slot has only one tag to respond, it is a successful slot. If there are two or more tags to respond, it is a collision time slot, and the value of Qfp is added with C value; if there is no tag response, it is an idle time slot, and the value of Qfp minus C value.
(4) The current slot processing is completed and the reader's slot counter is decremented by one. If the reader's slot counter is reduced to 0, the Querry command is sent again, a new frame is started, and step (2) is resumed; if the reader's slot count is not zero and the Q value changes, the message is sent. QueryAdjust command, adjust the Q value, open a new frame, return to step (2); if the reader's slot counter is not zero, and the Q value does not change, send the QuerryRep command, the value of the label slot counter is reduced Return to step (3). This cycle.
1.2.2 Performance Analysis of EPC Gen2 Anti-collision Algorithm
In the identification process, the parameter Q determines the range of random numbers generated by the tag. Parameter C determines whether to change the frame length to accommodate the change in the number of tags, thereby directly affecting the performance of the system. The algorithm does not consume a large number of operations to estimate the number of tags to be identified, but only to count the number of collision time slots and idle time slots. The Q value is incremented or decremented by 1 when the access channel continuously makes 1/C collisions or is idle. The algorithm is simple to implement, but it also has the following two disadvantages:
(1) The Q value repeatedly jumps.
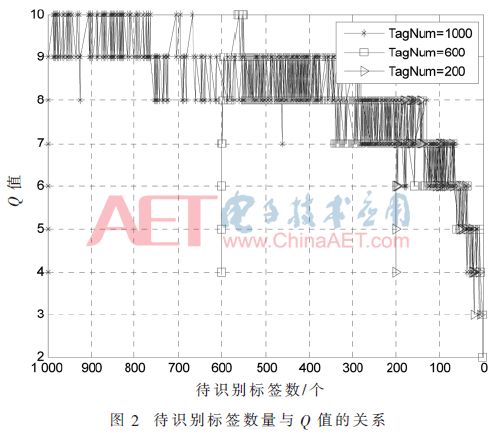
The standard stipulates that the initial value of Q is equal to 4, and when the number of tags is large, the Q value will increase to one value in turn, and it will repeatedly change around this value. Each time the Q value is changed, the tag has to regenerate a random number. Even if the Q value changes to a reasonable range (2Q is close to the number of tags), it will repeatedly jump, causing the tag to do a lot of useless actions and increase the recognition delay. For example, the relationship between the change in the number of tags to be identified and the Q value is shown in Figure 2 in the case where the number of tags is 200, 600, and 1,000.
(2) The frame length cannot be equal to the number of tags, resulting in a low throughput rate.
Since the frame length controlled by the Q value is always a power of 2, and the number of labels cannot always be a power of 2, the throughput rate of the algorithm must not reach a theoretical value of 36.8%. Because the C value has a direct impact on the throughput rate, and no specific value is given in the standard, different articles select different C values, and the throughput rate obtained from the analysis is also different. In order to facilitate the study, this article uses the literature [8] and adjusts the value of Qfp based on the empirical value of C=0.8/Q so that the system throughput can be maintained at about 32%.
2 The proposed optimization algorithm
The optimization algorithm InnerQ proposed in this paper is optimized for the two problems mentioned above. The InnerQ algorithm consists of two parts, one is the stable Q-value algorithm and the second is the collision time slot reprocessing algorithm.
2.1 stable Q value algorithm
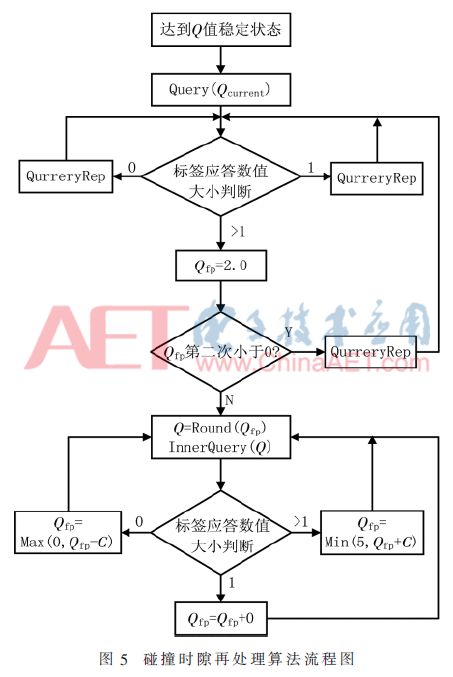
From the above analysis, it can be seen that when the number of tags is large, the Q value will increase from the initial value to a certain value, and then repeat around this value. A stable Q-value algorithm can be designed to record the change process of the Q value. Once the Q value is detected not to increase or decrease successively, but repeatedly to jump, the Q value is fixed so that the reader does not send QuerryAdjust repeatedly, resulting in all pending The identification tags repeatedly generate random numbers. The fixed state of the Q value is defined as a stable state of the Q value. The specific algorithm flow is shown in Figure 3.
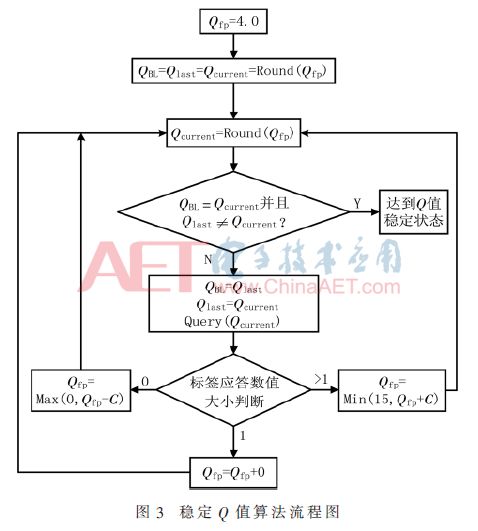
After the steady state of Q is reached, the distribution of label time slots is relatively decentralized, and the same time slot will not be selected for a large number of labels, and a large number of idle time slots will not occur, resulting in wasted time slots. The probability of successful tag access, collision, and idleness in a certain time slot [9] is shown in equation (1):

Equation (2) can be used to simulate the relationship between the total number of labels n and the Q value after the steady state is reached, and the average number of labels Nc in the collision time slot after the steady state is reached. The results are shown in Table 1.
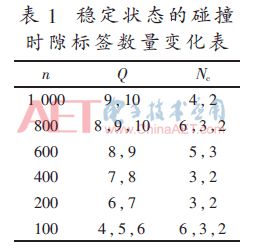
From Table 1, it can be concluded that when the Q value is stable, the distribution of labels is relatively scattered, and the number of labels for each collision time slot is small, ranging from 2 to 6.
2.2 Collision Timeslot Reprocessing Algorithm
After reaching the steady state of the Q value, only the time slot selected by the tag to access is dispersed, but there is still a collision tag. These tags need to be processed again before they can be fully identified. The solution proposed in this paper uses the original EPC Gen2 anti-collision algorithm processing logic for compatibility considerations, and it is a special DFSA algorithm, and the DFSA algorithm has a relatively high throughput when the number of tags is small. .
The proof process is as follows:
Let the frame length be L and the number of tags be n. The probability that a time slot is selected by only one tag is Ps, then:

The function image is shown in Figure 4. It can be observed that when the number of tags is less than 40, the throughput rate is significantly higher than 36.8%, and as the number of tags decreases, the throughput rate is greatly improved. This feature has been neglected by many scholars who have studied EPC Gen2 anti-collision algorithm optimization, and has not been fully utilized. As a result, the proposed optimization scheme always tries to approach the throughput rate close to 36.8%, but it cannot always exceed this theoretical bottleneck.
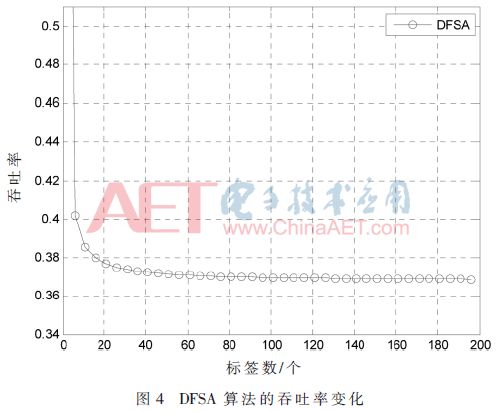
In this paper, we first use the above-mentioned Q-stability algorithm so that the number of tags in each collision slot averages between 2 and 6. The reprocessing of these collision tags does not affect the tags of other time slots. The DFSA algorithm has a high throughput when the number of tags is small, which greatly improves the throughput of the system. The algorithm flow chart is shown in Figure 5.
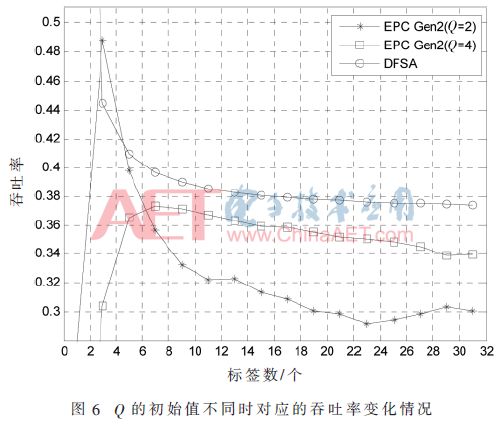
It should be noted that this paper uses the processing flow of the Q value in the original standard in the collision time slot reprocessing, but there are some changes. One of the obvious changes is that the initial value of the Q value should be changed from 4 to 2. Because the data in Table 1 shows that the number of tags in the collision time slot is between 2 and 6. When the Q value is equal to two, it is closer to the actual number of tags. Although it is not strictly equal to the theoretical value, the mathematical rule is consistent with the rule that the DFSA algorithm has a higher throughput rate when the number of tags is small. Figure 6 shows how the initial values ​​of different Qs correspond to changes in throughput.
3 Simulation Results and Analysis
In order to prove the effectiveness of the InnerQ algorithm from the experimental point of view, the simulation software MATLAB was used to simulate the EPC Gen2 algorithm, the DFSA algorithm, and the InnerQ algorithm. The number of tags is 1,000. Since all three algorithms are based on the improved randomness algorithm of the ALOHA algorithm, the simulation result is the average of 500 experiments. The three criteria of the system throughput rate, the number of collision slots, and the total number of slots are used as evaluation criteria, and the simulation results are shown in FIGS. 7 to 9 .
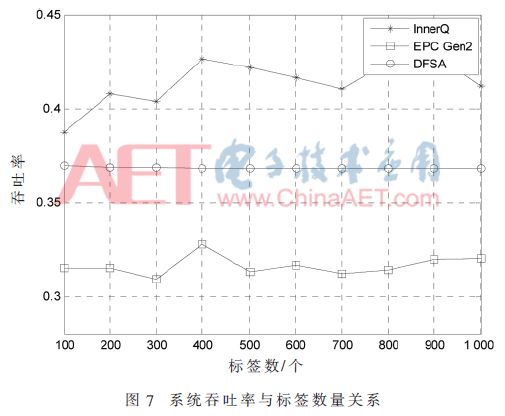
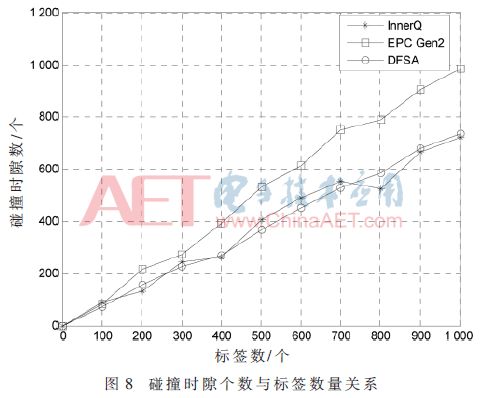
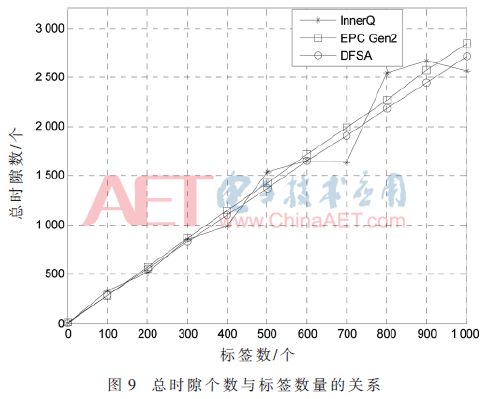
Figure 7 shows the number of tags from 100 to 1 000. The results show that the throughput of the DFSA algorithm remains at 36.8%, which is consistent with the theoretical analysis of this paper and previous research results. The InnerQ algorithm proposed in this paper combines the characteristics of DFSA algorithm with a relatively high throughput in the case of a small number of tags. Using the idea of ​​reprocessing collision time slots, the system throughput rate is stable at about 42%.
The results in Figure 8 show that the number of collision slots in the InnerQ algorithm is significantly smaller than the algorithm prior to optimization. Because the optimization algorithm makes the number of tags in the collision time slot relatively small, the probability of collision is smaller when this processing is performed again, and the number of collision time slots naturally decreases.
The results in Figure 9 show that the DFSA algorithm, the EPC Gen2 algorithm, and the InnerQ algorithm are not too large in identifying the difference in the total tag time slots, although the method of using the collision time slot reprocessing is actually equivalent to introducing more time slots. However, there are few labels in the collision time slot, and the Q value algorithm is stabilized, so that the Q value does not repeat the transition repeatedly, which is equivalent to reducing unnecessary waste of time slots. So the optimization algorithm does not add too many extra time slots as a whole.
4 Conclusion
This paper studies the characteristics of the DFSA algorithm and the EPC Gen2 algorithm, and points out that it is ignored by many people. From the theoretical and simulation data, it is proved that the optimization algorithm proposed in this paper can break through the original ALOHA class algorithm in the case of multi-label recognition. The highest throughput rate can only reach the bottleneck of 36.8%. The throughput of the optimization algorithm has been increased to about 42%, and the number of collision slots has also been greatly reduced. At the same time, compatibility with the current standards has been ensured, and it can be quickly put into actual production, which has a good application prospect.
Fan Control Board Pcba,Engineering Control Board Pcba,Control Board Pcba Assembly ,Control Pcba Assembly
Full Industrial CO.,ltd. , https://www.iotaindustrial.com